(알고리즘) 투포인터 + 슬라이딩 윈도우

코딩 테스트 심심치 않게 나오는
투 포인터 알고리즘과슬라이딩 윈도우에 대한 개념과 원리를 파악하고자 포스팅했습니다. 🧑🏻💻
투 포인터 알고리즘이란?🧐
투 포인터 알고리즘이란 이름 그대로 두 가지 포인터를 사용하여 문자열이나 배열에서 원하는 값을 찾는 방식이다. 대표적인 문제로는 연속 부분 수열 문제가 있다.
투 포인터 알고리즘 사용이유 💡
투 포인터 알고리즘 없이 무작정 탐색(반복문)을 사용하면 보통 이중 포문을 사용하면서 문제를 풀게 되는데 시간 복잡도 O(n2)이 넘어가며 너무 많은 시간이 걸리는 경우가 많다. 투 포인터 알고리즘은 반복문이 한번 돌기 때문에 시간 복잡도O(n)으로 더 효율적이다.
말로는 어떠한 방법인지 알기 힘들므로 밑에서 유명한 연습문제를 보며 설명해 보겠습니다.😁
투 포인터 알고리즘 예제 📝
N 개의 수로 이루어진 수열이 주어집니다. 이 수열에서 연속 부분 수열의 합이 특정 숫자 M이 되는 경우가 몇 번 있는지 구하는 프로그램을 작성하세요. 만약 N=8, M=6이고 수열이 다음과 같다면 12131112 합이 6이 되는 연속 부분 수열은 {2, 1, 3}, {1, 3, 1, 1},{3, 1, 1, 1}로 총 3가지입니다.
입력설명 🕵🏻♂️
첫째 줄에 N(1≤N≤100,000), M(1≤M≤100,000,000)이 주어진다. 수열의 원소값은 1,000을 넘지 않는 자연수이다.
입력예제 ✒️
10 5 1 2 3 4 2 5 3 1 1 2
해결방식 🗝
- 두 개의 포인터
lt, rt를 각각 0으로 세팅한다. - 연속 부분 수열의 합을 저장할
sum을 0으로 선언한다. rt위치가 증가하면서sum에rt위치의 값을 더한다.- 만약
sum값이 원하는 합보다 클 경우에lt위치의 값을 빼주면서lt를 증가시킨다. - 만약
sum값과 원하는 합의 값이 같다면answer를 1증가 시킨다.
동작방식 🐎
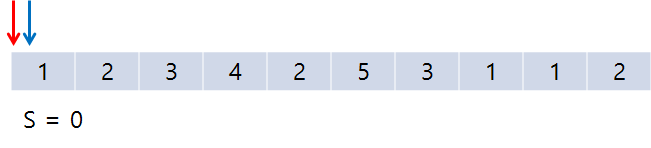
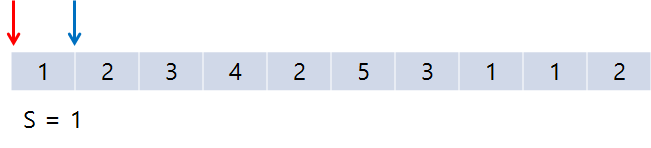
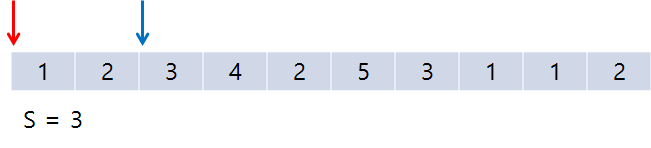
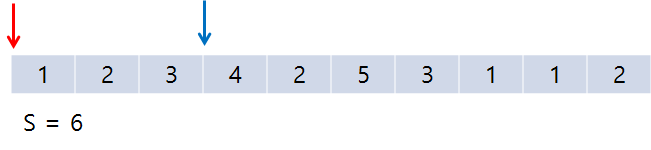
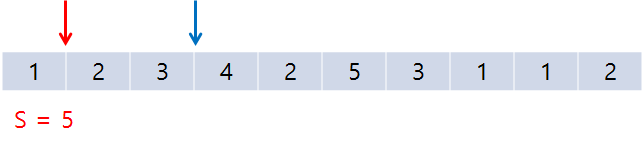
이런 식으로 5보다 작다면 rt를 증가시키고 크다면 lt를 증가시키면서 값을 구하다 보면 5일 때의 값이 나오게 된다. 그럴 때마다 answer의 값을 증가시켜주면서 반복문을 끝까지 돌면 된다.
투 포인터 알고리즘과 비슷한슬라이딩 윈도우(sliding window)라는 알고리즘도 존재합니다.투 포인터와 어떤 차이점이 있는지 밑에서 확인해 보겠습니다.
슬라이딩 윈도우(sliding window)란?🤔
마치 창문을 한쪽으로 밀면서 문제를 푸는 것과 모양이 유사해서 붙여진 이름이다. 투 포인터처럼 구간을 훑으면서 지나간다는 공통점은 있으나 어느 순간에도 그 구간의 넓이가 동일하다는 차이점이 있다. 구간의 넓이가 주어졌을 때는 슬라이딩 윈도우로 문제를 풀면 되겠다.
슬라이딩 윈도우(sliding window) 예제 📝
현수의 아빠는 제과점을 운영합니다. 현수 아빠는 현수에게 N일 동안의 매출기록을 주고 연속 된 K일 동안의 최대 매출액이 얼마인지 구하라고 했습니다. 만약 N=10이고 10일 간의 매출기록이 아래와 같습니다. 이때 K=3이면 12 15 11 20 25 10 20 19 13 15 연속된 3일간의 최대 매출액은 11+20+25=56만원입니다. 여러분이 현수를 도와주세요.
입력설명 🕵🏻♂️
첫 줄에 N(5<=N<=100,000)과 M(2<=K<=N)가 주어진다. 두 번째 줄에 N개의 숫자열이 주어진다. 각 숫자는 500이하의 음이 아닌 정수이다.
입력예제 ✒️
7 3 -3 3 1 -3 2 4 7
최대매출 해결방식 🗝
- 매출의 합을 저장할
res을 선언하고 첫 번째 인덱스 값부터 k까지의 값의 합을res에 저장한다. - K부터 N의 길이까지 증가시키면서 k의 인덱스 값을 더하고 k-k의 값을 빼준다.
- 반복문이 한번 돌 때마다
answer값과 현재의res값을 비교하면서 더 큰값을answer에 추가한다.
최대매출 동작방식 🐎
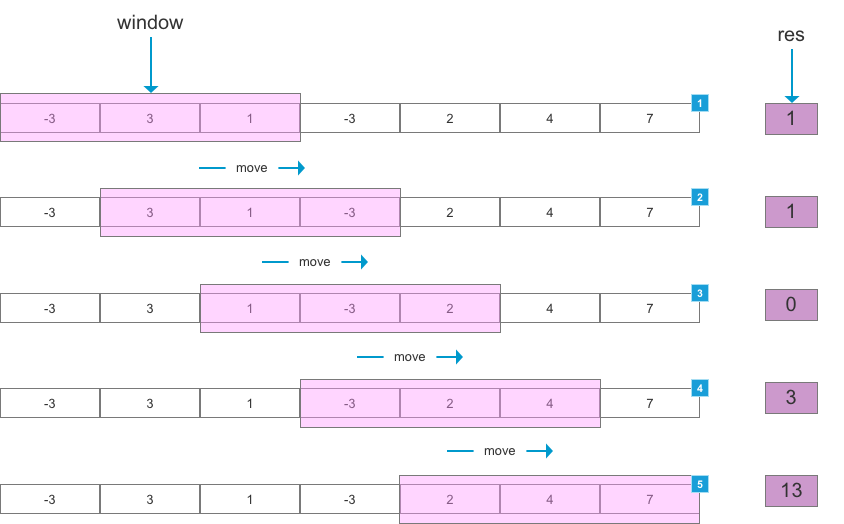
위에서 말한 해결 방식처럼 처음 시작은 k 길이만큼 -3,3,1을 res에 더해준다. 그런다음 다음으로 넘어갈때는 문이 미끄러지는 거와 같이 오른쪽으로 문이 1칸 가게된다. 그때의 res값은 -3을 더해주고 뒤에 값 -3을 빼준다. 이런식으로 쭉 진행한다면 반복문이 한번 다 돌면 값이 나오므로 시간 복잡도는 O(n)이 된다.
궁금하신 점이 있다면 아래 댓글로 남겨주세요!👇
